
Now it's time to pick one up and get flying.The Delhi Police on Friday designated a five-kilometre radius around the historic Red Fort as a "no kite flying zone'' till Prime Minister Narendra Modi hoists the tricolour at the Mughal era monument on Independence Day. That's all we have to know when it comes to the areas of kites. We can find the perimeter of the kite by adding all the side lengths together. As for CD and DA, we can use the Pythagorean Theorem too, where a = 2.5 and b = 12.5. If we remember our special triangles or the Pythagorean Theorem, we can find that.
This also means that DB = 15 cm (since the long diagonal is three times longer than the short one), and that DE = 15 – 2.5 = 12.5 cm. We know that AC is 5 cm long, which means AE = CE = BE = 2.5 cm. The question tells us Δ ABE and Δ CBE are congruent isosceles right triangles. That, and the fact that these segments are all hypotenuses of four right triangles. Luckily, our life is made easier since AB = BC and CD = DA.
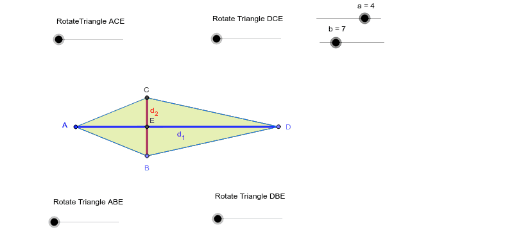
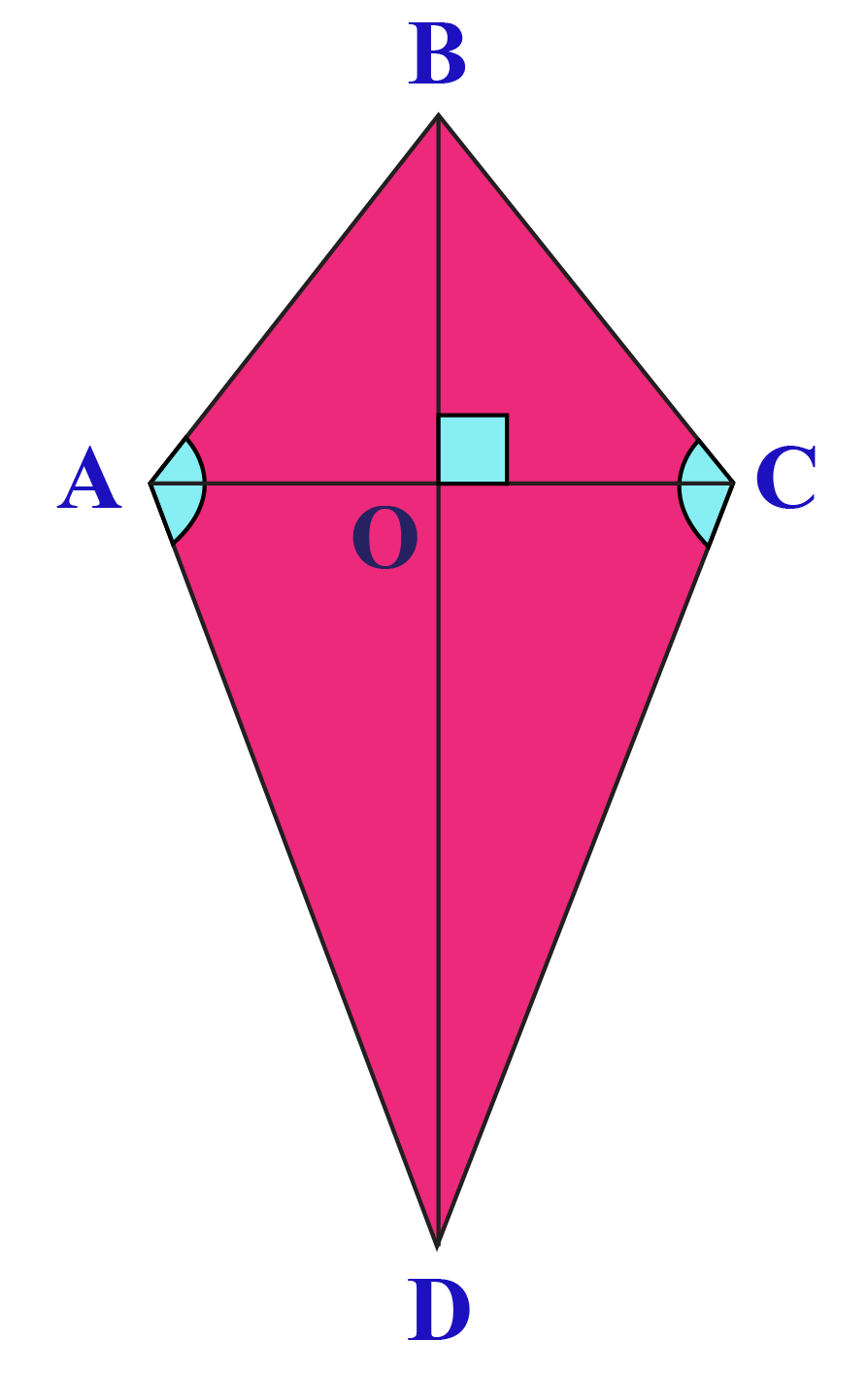
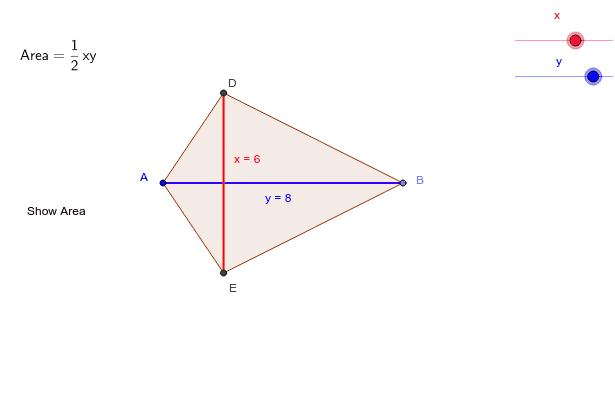
The perimeter is the sum of all the lengths of the sides, AB + BC + CD + DA. Does that help us find the perimeter? Sort of, but we need to use the other piece of information that we're given: the shorter diagonal splits the longer diagonal to make two isosceles right triangles. That means d 1 is 5 cm and d 2 is 3(5) = 15 cm long. Plugging in these values to the area formula should give us the lengths of the diagonals. If d 1 is a certain length x, then d 2 is three times that length, 3 x. Welp, we know that we have to use the area formula, but we should relate the two diagonals to each other first. If the area of the kite is 37.5 cm 2, what is its perimeter? The shorter diagonal splits the longer one so that two isosceles right triangles are formed. One diagonal of a kite is three times as long as the other. Kites can get pretty complicated, but don't get tangled. To find the area of a kite, we just need the length of the two diagonals. What is the area of a kite with diagonals of length 6 and 4? Even still, a couple thousand bucks wouldn't hurt. We have the two diagonals, and that's all we need, right? What is the area of the diamond's cross-section?Īll we need to do is apply the formula for the area of a kite. She requests the diamond be a perfect cut, with diagonals of 3 mm and 5 mm. Your fiancé would like you to buy her a $20,000 diamond with a cross-section in the shape of a kite. That means our final area formula for a kite ends up being relatively simple. Since we defined x and y so that x + y = d 2, we can replace the quantity in parenthesis with the second diagonal. Since the area of the kite is the area of the four triangles combined, we can just add up the areas of the individual triangles.
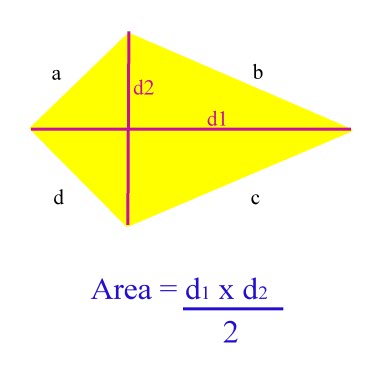
We'll just call the pieces x and y such that d 2 = x + y. We can split the vertical diagonal into two sections as well, but we don't know exactly what ratio. Diagonals split a kite up into two pairs of congruent right triangles, each with a base of, half of the horizontal diagonal. Let's take a look at this logically for a second. If we can use the diagonals of a rhombus to find the area, can we do the same with kites? If the two diagonals of a kite are perpendicular to each other (which they are), then we should be able to use the same type of formula. That's all good and fine, but it doesn't seem like any of that will help us find the area.īut wait. If all four sides of a kite are congruent, then we just have a rhombus. We already know that a kite is defined as a quadrilateral that has two adjacent pairs of congruent sides. The kites we're referring to probably aren't the ones that David Tomlinson was singing about. Whether you prefer diamond kites, fighter kites, or Hello Kitty kites (they're all the rage now), flying them can make dull windy days infinitely more enjoyable. There are few windy-day pastimes more fun than flying a kite.


 0 kommentar(er)
0 kommentar(er)
